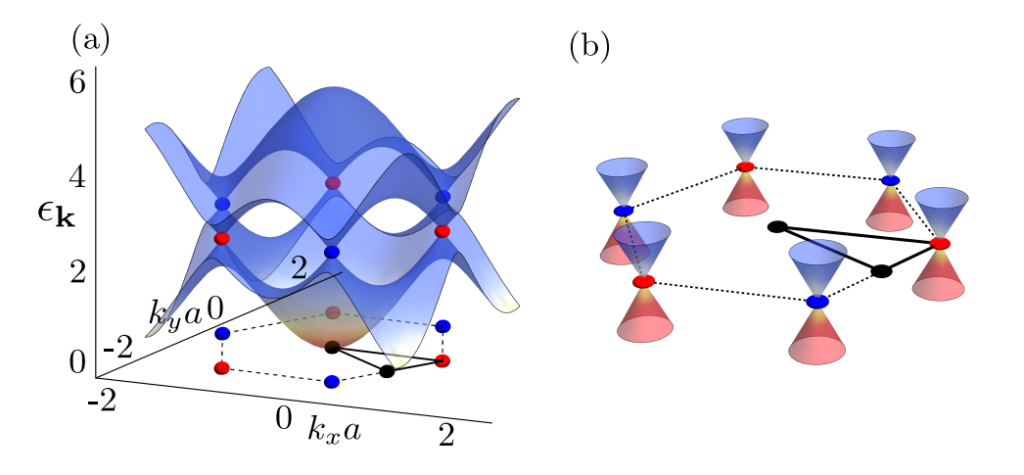
Dirac matter is any material where the low-energy excitation spectrum can be described by the Dirac equation (![]() ) rather than the more usual quadratic dispersion (
) rather than the more usual quadratic dispersion (![]() ). The excitations are typically fermionic, but may also be bosonic. The most well known and studied examples of Dirac matter are graphene and topological insulators (TIs), in which the Dirac particles are fermionic (electrons in graphene). While for fermionic Dirac matter, the dispersion around the
). The excitations are typically fermionic, but may also be bosonic. The most well known and studied examples of Dirac matter are graphene and topological insulators (TIs), in which the Dirac particles are fermionic (electrons in graphene). While for fermionic Dirac matter, the dispersion around the ![]() and
and ![]() points of the Brillioun zone can be examined using a linear approximation relative to the Fermi energy (b), in bosonic Dirac matter (a), the population of the particles is greatest at the
points of the Brillioun zone can be examined using a linear approximation relative to the Fermi energy (b), in bosonic Dirac matter (a), the population of the particles is greatest at the ![]() -point and the full description of the Brillouin zone is required; occupation of the
-point and the full description of the Brillouin zone is required; occupation of the ![]() and
and ![]() points requires pumping.
points requires pumping.
Systems described by the Dirac equation have many properties that are distinct from their ordinary counterparts, and a significant area of research is understanding the implications of the linear dispersion on transport and local properties. Further, the effects of scattering and the reaction of Dirac matter to external fields provide not only an indication of how the features of the Dirac spectrum may occur in real systems, but also provide a key insight into the origin of the very nature of, for example, topological insulators with their protected surface states.
Studying the renormalisation of the linear spectrum of both fermionic and bosonic Dirac quasiparticles in the interacting regime shows that both types of quasiparticle share significant commonalities, although the majority of studies consider fermionic particles. In particular, the self-energy correction for long range repulsion is not affected by the quasiparticle statistics – i.e.: bosons and fermions look the same, but differences due to the statistics are present in the behaviour of short-range coupled systems, giving rise to different thermal power law contributions.
Key Papers:
- Review article
Dirac Materials
T.O. Wehling, A.M. Black-Schaffer, A.V. Balatsky
Advances in Physics, Vol. 63, Iss. 1 (2014)
arXiv:1405.5774 - Universal trends in interacting two-dimensional Dirac materials
Saikat Banerjee, D.S.L. Abergel, H. Ågren, G. Aeppli, A.V. Balatsky
arXiv:1803.11480